
How to Bet: Correlation, Mean Regression, Expected Returns, and Position Sizing
Understanding the rules of probability—how to bet—can be a valuable asset for investors. Every day I come across investors who think that regression to the mean has nothing to do with correlation, who don’t bother to think about odds, and who take wild stabs at position sizing. Until relatively recently, I was such an investor myself. In this article I’m going to attempt to impart my understanding of these things and give some general hints as to how they can be applied to investing strategy; in my next article, which is part of my How to Be a Great Investor series, I’m going to apply my conclusions specifically to the art of investing.
A word of warning: I am approaching this problem very differently from the traditional approach, which builds on Harry Markowitz’s seminal 1952 paper “Portfolio Selection.” Markowitz began his discussion with a rejection of the rule that an investor should maximize expected returns. I don’t reject that rule at all. Markowitz proves mathematically that if we accept this rule, then “the investor places all his funds in the security with the greatest discounted value” and does not diversify at all. But his mathematical proof looks only at the expected return and not at the range of possible returns. Another way to put it is that his proof is perfectly valid for a small, one-time investment, but cannot apply to compounded and repeated large investments, for when every investment carries the risk, however small, of a 100% loss, the investor should never place “all his funds in the security with the greatest discounted value.” Following his rejection of the maximize-expected-returns hypothesis, Markowitz concludes that an alternative rule must apply: that the investor should “consider expected return a desirable thing and variance of return an undesirable thing,” and the bulk of his paper is concerned with finding an efficient balance between those two. I come at the subject from an entirely different perspective, since I view risk as the probability of permanent loss and view variance of returns as the natural result of low correlation between expected and actual returns.
A Hypothetical Problem
There are seven poker players. They just completed a tournament in Las Vegas, and we know in which order they were eliminated. Now, a week later, they’re about to play a different tournament in Atlantic City, and we are trying to predict which of them will outlast the others. Besides the order of elimination in Las Vegas, the only other fact we know is that in similar situations, there is usually a modest correlation between the positions of the players in the first tournament and those in the second. (Correlation, in this context, means sequential similarity. A perfect rank correlation is one in which the values are in the same order of size. A perfectly negative rank correlation is one in which the values are in the opposite order of size.)
You are required to bet on which poker player will win. You can make one and only one bet.
You have two conflicting impulses. On the one hand, obviously, some players are, in general, better than others, and this is proven by the modest correlation. Poker is not entirely a game of luck. Therefore, you should place your bets on the winner of the last tournament. On the other hand, obviously, there is some regression to the mean. A player that does extremely well in one tournament will probably not play quite as well in a second. Therefore, you should avoid placing your bets on the winner of the first tournament and instead place your bets on one who performed closer to average.
Which is the best strategy for placing your bets?
The Solution.
We have been told that there is usually some correlation between the positions of the players in the first tournament and those in the second, and we know this from the results of previous poker tournaments.
Regression to the mean is the precise opposite of positive correlation. Think of it this way. If the poker players were eliminated in exactlythe same order in Las Vegas and Atlantic City, the correlation would be perfect (1.00) and there would be no regression at all. And if the poker players were eliminated in exactlythe opposite order, regression to the mean would be perfect (the worst would do best and the best would do worst) and there would be a perfectly negative correlation (–1.00).
If we were to maximize our potential for winning, should we place our bets on the winner of the Las Vegas tournament, the runner-up, the third-place winner, or someone else? After all, with an imperfect correlation (less than 1.00), there is some regression going on, right?
Let’s say you were to generate an actual permutation table (and these can be absolutely huge: the number of possible permutations of ten players is 10!, or 3,628,800), measure the correlations of each permutation to the original order, and look at who has the best chance with each correlation to win. Here’s the correlation table for seven players, with the most likely winners in bold:

There are two surprising things about this result. First, a known correlation of zero is fundamentally different from an unknown correlation. If the correlation is unknown—you have no idea if it’s positive or negative—then every player has an equal chance of winning. But if the correlation is zero, then middling players are your best bets. Second, one might have thought that with a very small but positive correlation, the top player would remain the best bet; but that’s not actually the case.
The correlation table shows that you should place your bets on the top player when the correlation is high (above, say, 0.25), the worst player when the correlation is low (below, say, -0.25), the middle player when the correlation is 0, and some in-between player when the correlation is between 0.25 and -0.25.
For those who want to get into the weeds of measuring correlations, I’m now going to explain the mathematics of Kendall’s tau; feel free to skip this paragraph if you’re not interested. I use Kendall’s tau as my correlation measure because it’s less susceptible to outliers, easier to interpret, and more intuitive than the other standard measures of correlation, Pearson’s r and Spearman’s rho; in addition, with Kendall’s tau, you don’t have to deal with covariance or standard deviations. Take a pair of data points in the two series and classify it as concordant or discordant depending on whether the points are in the same order or the opposite order in the two series. Kendall’s tau is the number of concordant pairs minus the number of discordant pairs, divided by the number of all pairs. It ranges from 1 for a perfect correlation—all the pairs are in the same order—to -1 for a perfectly negative correlation—all the pairs are in the exact opposite order. If Kendall’s tau is 0.2, then there is a difference of one-fifth between the number of concordant pairs and the number of discordant pairs, and the only way you can split a whole into two parts with a one-fifth difference is three parts to two parts, so the odds of one player beating the other if she beat her in the first tournament is three to two. Similarly, if Kendall’s tau is 0.333, her odds will be two to one, and if Kendall’s tau is 0.5, her odds will be three to one. Obviously, if you know that one player was in first place and the other was in last place, the odds will be higher, and if you know that they were in third and fourth place, the odds will be lower. Kendall’s tau tends to be significantly closer to zero in most cases than Pearson’s r or Spearman’s rho. A Kendall’s tau of 0.25 might be a Pearson’s r of 0.35, for example.
Applying Correlation to Investment Strategies
In the above example, we’re talking about the correlation of the performance of players between different tournaments. We can now apply this lesson to the performance of investment strategies between different time periods or the correlation between expected and actual returns.
Let’s look at time periods first. The natural impulse of investors is to “chase performance.” Investors want to put their money into strategies that have performed well in the recent past. This makes perfect sense if the correlation between past performance and future performance is high. It makes no sense at all if the correlation is negative or close to zero.
So it’s worthwhile investigating exactly what that correlation might be. And that depends on two things: how different the strategies are and what time periods you’re looking at.
In my own experimentation, I have found that longer time periods are generally more correlative when it comes to performance. The most correlative look-back period for future three-year performance seems to be the previous ten to twelve years; I would guess that the most correlative look-back period for future ten-year performance would be the previous thirty to forty years (though I have not done the testing to establish this). Correlation is probably lowest when looking at a short period—five years or less—which is precisely what performance chasers usually look at.
If your investment strategies are limited to long-only equities, the performance correlation is going to be quite low—in the range of 0 to 0.3. Using alpha as a performance measure improves the correlation a little bit. If the strategies include fixed-income and long-short strategies, the correlation will likely be higher. If they’re limited to very diversified large-cap equity strategies, the correlation may well be negative. Actively managed mutual funds, for example, have a slightly negative correlation between performance over long periods.
One doesn’t have to look at past performance at all, though, in order to apply the lessons of correlation. One can use correlation as a proxy for confidence. Let’s say you can think of seven different investment strategies and can assign an expected return to each one based purely on your theory of how they will perform. Don’t stop there. Consider this: if someone you knew, with precisely your experience and depth of thought, were to assign expected returns to seven strategies, what do you think the correlation between present expected returns and future performance will be? Use that number as your correlation estimate.
My advice: With low correlation, spread your bets. Don’t chase short-term performance. Don’t optimize your strategy over a specific period. Don’t expect your estimation of expected returns to correlate perfectly with future performance, and take action accordingly.
This advice goes against my own impulses—and my own past practices. But I’m working to change those.
Spreading Your Bets
Let’s say you had the opportunity to bet $100 and you could put as much of that money on any player as you wanted, and let’s say the typical correlation between tournaments is 0.33. Would it be better to bet the entire $100 on the first-place winner of the Las Vegas tournament, or to spread some of your money around on the others?
That depends entirely on whether this is a one-time bet or a habitual bet, whether you’re making small bets or putting all your money on the line, and whether the payout is all-or-nothing or graduated.
Let’s look at the one-time, small-bet, all-or-nothing scenario first. (This is essentially the scenario that Markowitz examined at the outset of his seminal paper.)
In order to place bets wisely, it’s important to know what the expected return of each bet is. There are many ways to estimate odds, and one of them is to look at past performance. It is also, of course, important to take into account the payout schedule. For an all-or-nothing bet, the correlation table can be easily converted into a table of expected returns by taking each value, multiplying it by the number of players, and subtracting 1. Notice that the sum of each column is 0.

So if it’s an all-or-nothing bet and the correlation is 0.33, your expected return if you put all your money on the number-one player is 97%, and your expected return if you put all your money on the number-seven player is -90%. If you put a third of your money on the number-one, number-two, and number-three players, your expected return will be 70%. There is basically no way to spread your bets so that you can have a higher expected return than putting all your money on the number-one player.
However, if you are making a practice of placing bets like these and the bets are large (i.e., after each bet you put your entire returns on the line), diversifying and compounding will make a huge difference. In that case, you want to maximize the chance of not losing the entirety of your stake by spreading your bets proportional to your expected return.
Let’s say you spread your bets evenly, putting one-seventh of your money on each position. Because the total payout is just as much as the amount you bet, you’ll break even every time you bet.
Let’s say you put one-fifth of your stake on the first five positions and nothing on the others. Then every time one of the two losers wins, you’ll lose 100% of your stake.
But if you place your bets proportionally to your odds—if you spread your $100 so that you put $28 on the first position and only $1 on the seventh, and divide your next bets in the same proportion—you’ll do extremely well. If the odds hold out, you’ll average 30% per bet. (The actual optimal bet size by position is $28, $25, $20, $14, $8, $4, and $1.)
Now all of the above applies only to all-or-nothing bets. With an all-or-nothing payout, you want to spread your bets proportionally to the expected return (in other words, add 100% to each expected return and divide by the number of positions) to maximize your take. The mathematical demonstration of this is pretty nifty, if you’re into that kind of thing.
What About Lower-Risk Payouts?
The above scenario is inappropriate for an activity like investing, where the payouts are rarely such high-risk. The all-or-nothing scenario is like investing in seven companies, one of which will pay off 600%, and the other six of which will go bankrupt, and then doing it again and again. High-risk payouts are a good starting point for computation of probability, correlation, and position sizing. So let’s take what we’ve learned and apply the lessons to lower-risk payouts.
If the payout is graduated, as it is with investing, then the calculation of expected return is far more complicated, as you’d have to take into account not just the chance of each player winning, but also each player placing second or third or fourth, etc. So, for example, let’s take the following payout schedule. If you pick the #1 winner, you get a 40% return on your bet; if you pick the #2 winner, you get a 30% return; #3 pays 20%; #4 pays 10%; #5 and #6 pay nothing; and if you bet on #7, you lose 100% of your money. Now the odds are much more similar to what you might get by investing in seven different stocks with a one-out-of-seven chance that they’ll go bankrupt.
Let’s say the estimated correlation between past and future performance (or expected and actual returns) is 0.238 (per the above table). Then the expected returns on the seven players are as follows:
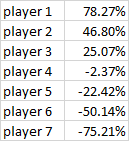
Now, if your bets are long only, your optimal bets would be around 40% on player 1, 27% on player 2, 18% on player 3, 8% on player 4, 5% on player 5, 1% on player 6, and nothing on player 7. (The calculation of these optimal bet sizes can no longer be expressed with a simple formula, but is extremely complicated.)
Notice that you’re not placing all your money on the past winners, which is what we have a tendency to do. But you’re also not spreading your bets as thinly as you would if you were risking all your money on six out of the seven players. Now there’s a large difference between the expected return and the optimal position sizing.
The scenario changes significantly if you’re allowed to use unlimited margin and go short. In that case (assuming no interest charges), the optimal bet sizes are very approximately 150%, 120%, 105%, 50%, -50%, -65%, and -190%.
Now what if you’re a very conservative investor and would prefer to keep half your money in reserve? (This situation is equivalent to judging that none of the stocks you invest in will ever go bankrupt and that your downside is limited to a 50% loss.) In that case, your bet sizes need to double (proportionally, that is) in order to make the same return. Take the original optimal bet sizes, multiply by the number of positions, and subtract 100%. Now double everything. Then reverse the process, adding 100% and then dividing by the number of positions. If you can’t go short, you’ll have no way to replicate the optimal return of the above scenario; if you can, your bet sizes will increase substantially.
Conclusions
Here are, perhaps, the most important general points from this understanding of probability, correlation, and position sizing.
- Mean regression and correlation are precise opposites.
- If correlation is high, the winner of one series is going to be the most likely winner of the next. If correlation is well below zero, the loser of one series is going to be the most likely winner of the next. If correlation is between -0.25 and 0.25, middling players are most likely to win.
- When making small, infrequent bets, always bet on the position most likely to win. When making large, frequent bets, calculate optimal position sizing if you can, based on the expected payout and your estimate of the correlation between past/expected returns and future returns.
- As your risk is reduced—either because of graduated payouts or because you’re putting less of your money at risk—your position sizing should be more aggressive, even to the point of shorting the positions you have the least confidence in.
All of these points should make intuitive sense. Perhaps it’s good to know that they’re backed by solid mathematical foundations.
In my next article—How to Be a Great Investor, Part Five: Think Probabilistically—I’ll be applying what we’ve learned here to some more practical investing scenarios.
