What Are the Best Value Ratios?

I recently performed a study of over fifty different value factors to see which performed the best. (Admittedly, a lot of them are similar.) The results surprised me.

Method

I conducted the study using a web-based stock research company called Portfolio123. Here’s my methodology. (This gets a bit technical; feel free to skip to the next paragraph if you’re not interested in the details.) First, I used a universe of all US and Canadian stocks with a price greater than $3, a median daily dollar volume greater than $50,000, and excluded unlisted stocks and MLPs. I then tested the decile performance ranks of each factor both over the last ten years and since 1999, assuming slippage-free monthly rebalancing. (What does that mean? It means I formed ten portfolios according to the rank of each stock on the value ratio in question, so that if a stock ranked in the top 10% it was in the first portfolio, if it ranked in the second 10% it was in the second, and so on. These portfolios were reconstituted every four weeks according to each stock’s rank at that time. The performance of these portfolios was measured and annualized.) I then took these decile performances and measured the slope of their linear regression. (What does that mean? I lined up all the decile performances and used those as my y values, my x values being 0.1, 0.2, 0.3, . . . 1.0. I then calculated the linear regression—in other words the line that best fit these performance numbers—and calculated the slope. If all the decile performances are each one higher than the last, this slope approximates the difference between the performances of the bottom 10% and the top 10%; if they’re more variable, the slope diminishes.) The top performers had not only the greatest differences between the top and bottom decile, but the smoothest slope in-between. I also considered only the top decile in terms of performance, since most people use value ratios to go long, as well as the Sharpe ratio of that top decile. Lastly, I performed this exercise using both Compustat’s and FactSet’s data.

In this article, I want to discuss the value factors that really consistently outperform. They performed well in the last ten years and in the last 23. They have steep bottom-to-top slopes and the top decile is not only a strong performer but has a high Sharpe ratio. They did well both with Compustat and with FactSet data. These are factors that I think are difficult to go wrong with.

The Metrics of Value Ratios

Before we start with those, I want to talk a little about what numbers we should rely on for value ratios. Should we just look at the most recent quarter? The trailing twelve months? The last three years? The last five? Or should we look at analyst estimates instead? And if so, for the current fiscal year, or for the next twelve months, or the next fiscal year?

While there are no wrong answers, I would suggest that the most important values are, in order of importance, the current fiscal year’s estimate, the next twelve months’ estimate, the trailing twelve months’ GAAP figures, and the most recent quarter’s GAAP figures. But a lot depends on your holding period. If you’re a buy-and-hold investor, looking at the most recent quarter will simply result in a lot of churn. If you tend to rebalance more frequently, as I do (I rarely hold a stock more than a year), then the most recent quarter can provide some good guidance.

Ratios all consist of a numerator and a denominator. If market cap, price, or enterprise value is in the numerator, you get a valuation ratio where lower numbers are better. The classic example is P/E (price to earnings), but I’m sure you’re familiar with price to sales, price to free cash flow, and EV to EBITDA. If market cap, price, or enterprise value is in the denominator, you get a valuation ratio that’s called a yield, where higher numbers are better. The two appear to be equivalent, but they’re not. A company with a high P/E may be overpriced, but not as overpriced as a company with a negative earnings yield. Let’s compare three companies, each selling for $20 a share. One has a trailing twelve-month (TTM) EPS of $4.00, one has an EPS of $0.50, and one has an EPS of –$1.00. The first has a P/E of 5, the second has a P/E of 40, and third doesn’t have a P/E at all. Which is a better buy, the second or third company? P/E doesn’t really tell you, in a strict mathematical sense. Earnings yield, however, allows you to rank companies with negative earnings lower than companies with low but positive earnings, and allows you to compare two companies with negative earnings. In fact, companies with barely negative earnings yields significantly outperform companies with extremely negative earnings yields.

Capital Structure and Value Ratios

Why do we compare a company’s earnings to its price but its EBITDA to its EV? Why do we have two different versions of free cash flow, depending on whether we compare it to market cap or enterprise value?

Let’s take an analogy. You buy a house for $500,000, paying $100,000 down and getting a loan for $400,000. You collect $50,000 a year for renting the house, and you pay $20,000 a year in mortgage costs.

There are four possible ways you can look at your earnings. You can simply ignore the debt entirely and divide $50,000 by $100,000 and say you’re getting a 50% yield on your investment. Of course, this is garbage: you’re definitely not. You can deduct the mortgage costs from your $50,000 but also base your yield on the $500,000 the house is worth and say you’re getting a 6% yield on your investment. This is also garbage: you’re deducting your debt twice, once for the interest expense, and once for the $400,000 you owe. Your actual yield is far higher than that.

Here are the other ways to calculate your yield. The first is comparable to earnings yield: you subtract your mortgage costs from the rent you earn and divide by your cash outlay, $100,000, for a 30% yield. The second is comparable to EBIT/EV: you don’t subtract your mortgage costs and divide the $50,000 rent by the entire $500,000, for a 10% yield.

Are those at all commensurate? Indeed, they are. You’re getting a 30% yield on your cash, but a negative 5% yield on your debt. And you have four times as much debt as you have cash. So if you deduct four times 5% from your 30%, you come up with 10%—exactly the same as your EBIT/EV–based yield.

(I probably should have used after-tax numbers in this example, but I wanted to keep it simple.)

The lesson here is that if you’re comparing something to a company’s price or market cap, that “something” has to be an after-debt-related-expenses number. Operating income, EBIT, or EBITDA are not allowed. And if you’re comparing something to a company’s enterprise value, that “something” has to have the interest expense added back to it if it was deducted earlier. That’s why we add the taxable portion of interest expense back to free cash flow if we want to compare it to enterprise value. (Technically, we should also take into account debt issued and debt repaid if the company issues or repays debt regularly.)

As for which to use, it depends on what you’re looking for. If you’re just interested in knowing how expensive your shares are, then don’t bother with enterprise value, since the value of your shares is an equity value and has nothing to do with a company’s debt. But if you’re interested in how valuable the company is, then enterprise value is the way to go.

A warning: never use enterprise value–based ratios for companies in the financial sector. For a good number of those companies, the more debt they issue, the higher their revenue.

As an investor, I’m interested in looking at a company from as many angles as possible. I therefore pay attention to both price-based ratios and EV-based ratios.

Free Cash Flow Yield

The best value factors I found are all variations of free cash flow yield. (I’m not the only one to reach this conclusion: another blogger, Harry Turner, arrived at this result using entirely different methods.)

A few years ago I wrote an article about free cash flow, which you can read here. I suggest you follow that link before continuing with this section. It’s a good guide to free cash flow’s history and the various ways of measuring it. A much more comprehensive guide is Aswath Damodaran’s, which he published recently here.

Free cash flow yield is simply free cash flow divided by market cap, or free cash flow per share divided by price. But there are a number of variations that work equally well or better, and they’re all worth discussing.

1. Measuring free cash flow. The standard measure is operating cash flow minus capital expenditures. (In P123 language, that’s simply FCF.) But there are several good alternatives. Many, including Warren Buffet, maintain that you should only subtract the capital expenditures spent on maintenance, not growth-related capital expenditures. Most companies don’t separate out these two, so it takes some digging—and estimation—to get to the right number. Others go to the opposite extreme and say that you should subtract not only capital expenditures but all other investing-related cash flow, which includes acquisitions. (In P123 language, that’s OperCashFl + CashFrInvest.) Complicating this is that many companies will list major asset purchases as capital expenditures, yet when they sell those same assets they don’t deduct them from capital expenditures but instead list them as other items in the investing portion of the cash flow statement. Yet another way to measure free cash flow is EBITDA (or EBIT) minus capital expenditures (Michael Mauboussin favors a variation of this method; in P123 language, that’s EBIT - CapEx or EBITDA - CapEx). This measure cannot be used with market cap or price, and must be used instead with enterprise value. Many others believe that you should deduct not only capital expenditures but also dividends paid, since that is a better measure of what’s left over to fund a company’s growth. (In P123 language that’s NetFCF.) Lastly, as I stated above, you have a wide choice between estimates and GAAP figures over various time periods. Taken all together, there are more than twenty different ways to measure free cash flow. I don’t have any strong preference between them, and find them all quite valuable measures. But below I’ll tell you which specific measures performed the best. (There is some debate over whether free cash flow ratios are effective for companies in the financial sector. From my research, they definitely are, and sometimes will function even better than earnings yield.)
2. Market cap or EV. It’s generally a little more useful, in my opinion and experience, to compare free cash flow to enterprise value than to compare it to price or market cap. But in order to do so, you have to add back the company’s interest expense. (If you’re using EBITDA or EBIT minus capital expenditures, you don’t have to worry about this because these are pre–interest expense numbers.) Because free cash flow is an after-tax measure, you only want to add back interest expense after taxes, or interest expense times one minus the company’s tax rate (or the industry’s tax rate, or some measure of the effective tax rate of the country’s companies, depending on your preference). (My preferred measure, in P123 language, is IntExpA * (1 - TaxRate%TTMInd/100)). And, once again, never use EV-based ratios for companies in the financial sector.

The Best Variations of Free Cash Flow Yield

Below are the variations of free cash flow yield that performed the best in my tests. I’m listing them from the simplest to the most complicated, with the market-cap-based ratios first, followed by the enterprise-value-based ratios.

1. Free cash flow yield. This is simply free cash flow divided by market cap, using TTM values. FCFTTM / MktCap
2. Estimated free cash flow yield. Here you use analyst estimates for the current fiscal year in place of TTM GAAP values. But if those aren’t available, use the TTM values. IsNA (FCFEstCY, FCFTTM) / MktCap
3. Net free cash flow yield. Here you subtract the dividends paid from the TTM free cash flow. NetFCFTTM / MktCap
4. Net free cash flow yield minus equity costs. Here you take the net free cash flow and subtract the cost of equity times the invested equity. There are a lot of different ways to measure cost of equity. The simplest is the risk-free rate plus the company’s beta times an equity risk premium. (I use the ten-year treasury yield as the risk-free rate and 10% minus that yield as the equity risk premium.) A much more complicated method is the subject of another article I wrote. By “invested equity” I mean book value less cash and equivalents. (NetFCFTTM - (Close (0, ##UST10Yr) / 100 + (0.1 - Close(0, ##UST10Yr) / 100) * Beta3Y) * Max (0, AstTotQ - IsNA (CashEquivQ, 0) - IsNA (LiabTotQ, DbtTotQ))) / MktCap
5. Unlevered free cash flow to enterprise value. Unlevered free cash flow is free cash flow plus the taxable portion of interest expense. I use TTM GAAP values. Enterprise value is market cap plus total debt minus cash and equivalents. (FCFTTM + IntExpTTM * (1 - TaxRate%TTMInd/100)) / EV
6. Estimated unlevered free cash flow to enterprise value. Here you use the current fiscal year’s estimate instead of the TTM GAAP value when it’s available. (IsNA (FCFEstCY, FCFTTM) + IntExpTTM * (1 - TaxRate%TTMInd/100)) / EV
7. Either of the above minus cost of capital. Here you calculate the weighted average cost of capital as follows. Take the cost of equity (as outlined in #4 above) and multiply that by the market cap; add to that the cost of debt, which is the average yearly interest expense; then divide that sum by the sum of market cap and debt. This is the WACC, which you should multiply by invested capital. Invested capital is total assets minus cash and equivalents and minus non-debt current liabilities. (FCFTTM + IntExpTTM * (1 - TaxRate%TTMInd/100) - (((Close (0, ##UST10Yr) / 100 + (0.1 - Close(0, ##UST10Yr) / 100) * Beta3Y) * MktCap + IntExp5YAvg) / (MktCap + DbtTotQ)) * (AstTotQ - CashEquivQ - IsNA (LiabCurQ - DbtSTQ, 0))) / EV

Which of these seven had the absolute best performance? Well, they’re all very close, but if I had to choose just one, it would be #6, with #3 in second place.

A Word About Deducting Costs of Equity and Capital

I’ve devoted a lot of my writing to Michael Mauboussin, one of the most perceptive investor/analysts working today. He and Dan Callahan recently published a paper called “Return on Invested Capital: How to Calculate ROIC and Handle Common Issues,” which I suggest you read. It’s a terrific introduction to his thought on one of his key measures, return on invested capital.

Near the beginning of the paper, Mauboussin and Callahan point out that there’s a very strong correlation between a) the difference between return on invested capital (ROIC) and the weighted average cost of capital (WACC) and b) enterprise value (EV) divided by invested capital (IC). See Exhibit 1, the chart on page 2 of the paper, which I take the liberty of reproducing below.

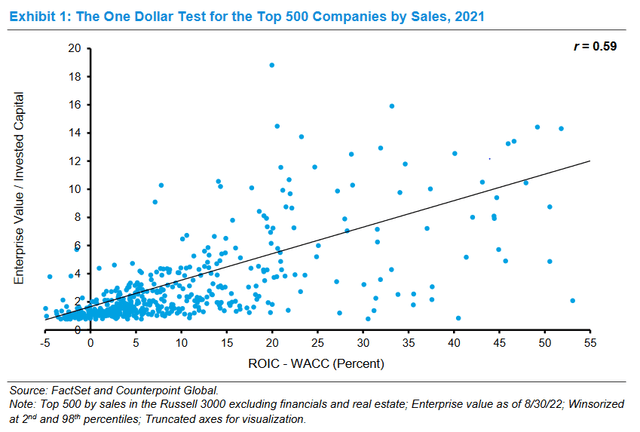
My idea was: why not use this correlation as the basis of a value ratio? If ROIC – WACC is proportional to EV / IC, then EV is proportional to IC × (ROIC – WACC). And since ROIC = NOPAT / IC (where NOPAT is net operating profit after taxes), then EV is proportional to NOPAT – WACC × IC.

If, instead of NOPAT, we use free cash flow, then a good value ratio would be FCF – WACC × IC. So I tried that. The results were very encouraging, and were, in fact, significantly better than using NOPAT. That’s why I deducted the costs of capital and equity in formulas number 4 and 7 above.

Conclusion

I think it’s very telling that the value ratio that seems to work the best, according to my methods of testing, is the one most deeply rooted in valuation methodology.

In fact, it works better than any automated intrinsic value method that I’ve tried. I have a theory about why that is.

Projecting growth rates based on past growth is almost impossible. Verdad, an asset management firm, publishes frequent research notes, and they recently found that persistence of growth is entirely chimerical.

In addition, cost of equity is notoriously difficult to calculate or estimate, as I have discussed at length.

If companies have utterly unpredictable growth trajectories and if cost of equity is more or less chimerical, we could assign all companies the same growth and the same cost of equity. Then intrinsic value calculation becomes extremely simple, and uses only one or two variable inputs: free cash flow and, for EV-based calculations, cost of debt.

That, I believe, is why free-cash-flow-based valuation ratios work so well.

Some Exceptionally Cheap Companies

Using these ratios, here are the cheapest companies right now (as of 12/17/22) in Portfolio123’s “Easy to Trade North America” universe (listed stocks whose primary listing is in the US or Canada with a minimum price of $3 and a minimum daily dollar volume of $50,000, excluding MLPs), using a combination of FactSet’s and Compustat’s data: Friedman Industries (FRD), Vir Biotechnology (VIR), PBF Energy (PBF), Zim Integrated Shipping Services (ZIM), and Insignia Systems (ISIG). All of these have free cash flow yields above 40%. Now some of these may be cheap for good reasons. I believe that you should look at a lot more than just value factors when you’re choosing investments. So here are some other stocks with very high free cash flow yields (above 10%) that I consider especially safe investments (I own shares in all of these): Genie Energy (GNE), Limbach (LMB), Hammond Power Solutions (HPS.A:CAN/HMDPF), PrimeEnergy Resources (PNRG), and RCM Technologies (RCMT). All ten of these stocks are certainly underpriced by the measures I’ve discussed, and may well be worth your attention.

And if you want to short some stocks with extremely negative free cash flow yields (all below -40%), check out Kodiak Sciences (KOD), Groupon (GRPN), Aspen Aerogels (ASPN), Hippo (HIPO), and bluebird bio (BLUE). These aren’t the absolutely worst stocks in terms of free cash flow yield, but they’re companies with almost nothing else going for them either.

Disclosure: I have a beneficial long position in the shares of GNE, LMB, HMDPF, PNRG, and RCMT through stock ownership.