
A Tale of Two Volatilities
What We Talk About When We Talk About Volatility.
When we as investors talk about volatility, we’re usually talking about variability in price returns. If an investment goes up and down 5% to 10% per day, that’s high volatility; if it goes up and down 0.05% to 0.1% per day, that’s low volatility. It’s a relatively simple concept, and is traditionally measured using standard deviation.
But when we compare investments to each other, we start talking not only about variability in price returns, but also about beta. And the implicit assumption is that beta measures something very different from variability. Beta is market-related risk; variability is unrelated to the market. For example, one writer, whom I won’t name because of my respect for him, wrote recently, “Beta is magnificent in theory but unstable and erratic in practice. . . . Imagine a debt-heavy gold mine whose stock soars in a dull market because of news of a big find. Beta is low or maybe negative, because the move is out of sync with the market, but risk is still massive!”
There’s one major problem with this kind of thinking. Even if the gold mine’s stock was almost completely uncorrelated to the market, its beta would be lower if its price variability was lower. This article will explain why.
Why Beta and Variability Are Interdependent.
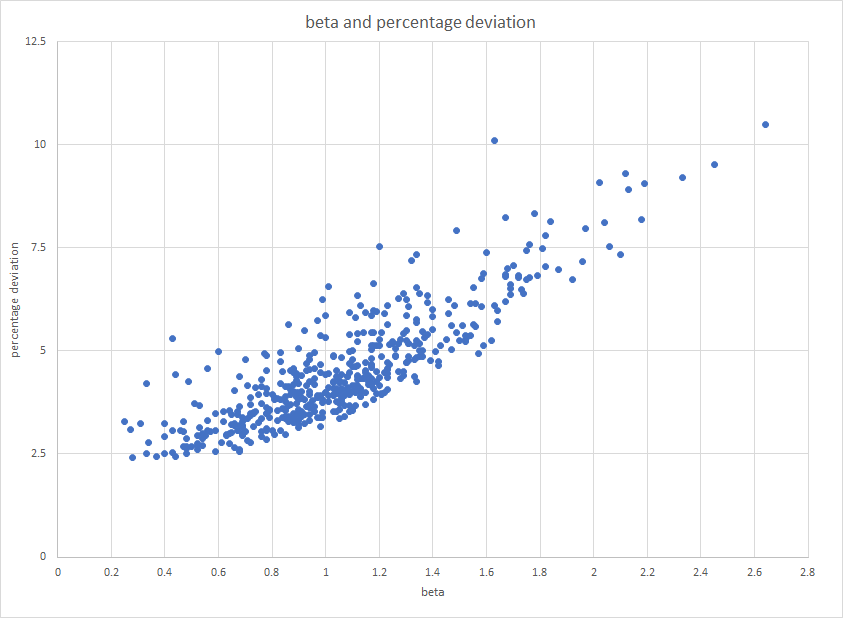
It can be observed empirically that the lower the beta of a stock’s returns is, the lower is the standard deviation of its price returns. Below is the three-year beta of the S&P 500 graphed on the x-axis and the three-year percentage deviation of the weekly price returns on the y-axis. (All figures are obtained from Portfolio123; beta is here calculated by comparing the weekly returns over the last 150 weeks to those of the S&P 500 without subtracting a risk-free rate from either one and percentage deviation is calculated by taking the standard deviation of the weekly returns over the last 150 weeks.) The relationship is very clear.
The reason for this is simple. Beta is the slope of the linear regression of a stock’s returns to a benchmark’s returns. The equation of the slope of a linear regression is
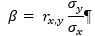
or, in plain English, the correlation of returns times the standard deviation of the stock’s returns divided by the standard deviation of the benchmark’s returns. Since the standard deviation of the benchmark’s returns is fixed (it’s the same for all stocks), the slope has a largely positive relationship with both the correlation and the standard deviation of the stock’s returns.
As beta goes to zero, two things could be happening: either the correlation goes to zero, or the standard deviation of the returns goes to zero. A stock whose price never changes has a beta of zero, just like a stock whose price changes in a manner that’s completely uncorrelated to the benchmark.
Now notice there’s a huge amount of white space at the bottom right of the graph. Why, for instance, are there no stock returns with a standard deviation of 5% and a beta of 2?
It’s because rx,y (the correlation between the market’s returns and the stock’s returns) cannot be greater than one. So how small can σy (the standard deviation of a stock’s returns) go? If we rearrange the above equation, we get
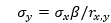
The higher the correlation, the lower σy can get, but the lowest it can ever get is σxβ, and since σx= 2.56% (the percentage deviation of the S&P 500), a stock with a beta of 2 can never have a standard deviation of less than 5.12%.
What About Negative Betas?
If we introduce short ETFs to the picture, we will get negative betas, and that’s because we’ll have negative correlations. With negative correlations, the higher the standard deviation of the ETF, the lower the beta. In other words, the relationship between beta and standard deviation is V-shaped with the lowest point at zero. After all, standard deviation, being the sum of squares, can never be negative.
This chart shows a sample of the betas and percentage deviations, measured exactly like in the above S&P 500 chart, of 1,600 ETFs, many of them leveraged and short.
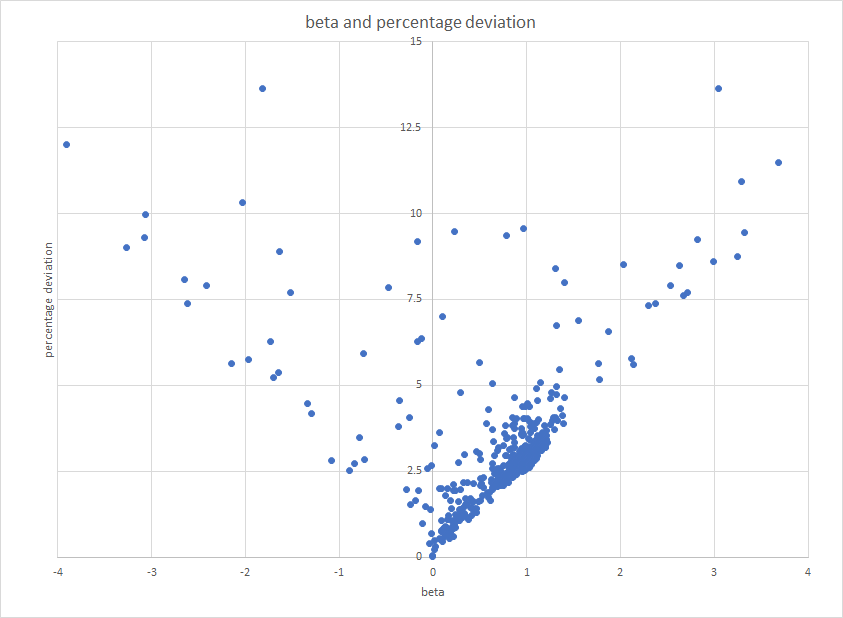
Note the slopes of the edge of the plots, which are ± 2.56%—the percentage deviation of the S&P 500.
What Does All This Imply for Low-Volatility Investing?
Judging from empirical data, low-beta and low-variability equity portfolios have both historically outperformed high-beta and high-variability equity portfolios. Portfolios based on beta and on variability are quite similar in constitution because of the interrelationship of these factors. The scale of their outperformance is consequently similar. With monthly rebalancing and no slippage costs, the lowest 20% of the Russell 3000 in terms of variability outperformed the highest 20% by 616.32% over the last twenty years (10.35% annualized); the lowest 20% in terms of beta outperformed the highest 20% by 540.28% (9.73% annualized). There’s not much difference there. The numbers for the S&P 500 are similar: 9.34% annual outperformance for low variability; 10.57% annual outperformance for low beta. Many studies have gone back close to a hundred years and have also looked at non-US markets. The results are strong.
There is a mathematical reason why low-beta equity portfolios outperform: as I have proven, in markets in which returns tend to be positive, alpha and beta are inversely correlated by their very nature. As far as I can tell, there is no mathematical reason why low-variability equity portfolios would outperform high-variability ones.
This outperformance goes against modern portfolio theory, which posits that investors demand greater return for greater risk. By any measure, low-volatility portfolios are less risky than high-volatility portfolios. Why should they outperform?
One theory is that investors tend to overpay for “exciting” stocks and ignore “boring” stocks, and “exciting” stocks clearly have more price variability than “boring” ones. But there seems to be no correlation between value stocks and low-volatility stocks, and this theory depends on one. There are a number of other theories out there, including a “stocks as lotteries” hypothesis. I haven’t found any of them very convincing—certainly not convincing enough to explain outperformance of such magnitude.
It’s possible that low-variability equity portfolios outperform simply because they tend to have low betas. But in that case, the outperformance of low-beta portfolios should be more apparent than the outperformance of low-variability portfolios, and that is not what we see. So there’s probably another reason as well. It merits further investigation.

The following comment is from Marc Gerstein and was posted on Seeking Alpha:
??????? For the record, I’m the un-named individual Yuval quotes in the first paragraph and there is absolutely nothing wrong with what I said.
So there are commonalities between beta and volatility . . . well, DUH!!! Whoever said they were distinct. They are each different flavors of the same phenomenon. But as I said, and as anybody who looks at specific stocks will easily recognize if one does it enough, Beta can be misleading because it’s tempting to forget the ” . . . relative to the market thing” and draw an erroneously conclusion Indeed, the chances of error are quire high since many web sites that offer free information to investors only show Beta and don’t show volatility.
Meanwhile, Hans Koolschijn asks: “Could there be a relationship between company characteristics (for example: variability in operating margins, ROA) and variability in price?”
YES!!! ABSOLUTELY POSITIVELY. Beta, Volatility and other metrics are ethereal . . . they don’t really exist in and of themselves. They are convenient descriptions of other things that do exist. Beta and volatility are different ways to describe something that does exist — stocks that bounce around a lot as opposed to having narrow bands within which they usually trade. But no intelligent investor4 can stop there. It’s essential to understand WHY thse differences occur. Well, let’s work our way up. Stocks respond to a measure of corporate wealth generation (usually eps) and sentiment about the earnings steam (the multiple of EPS). Companies in volatile lines of business tend to have more volatile sales patterns and that reflects down to earnings. The cost structure of a company contributes to that. The larger the portion of a company’s costs that are fixed or stepped (fixed within ranges that step up or down with changes in scale), the greater the impact on the bottom line of changes in sales. Smaller companies tend to be more volatile as they suffer comparatively from diseconomies of scale. Generally, higher margin and higher ROE companies tend to be more stable. Ditto companies with stronger balance sheets. And then., we have sentiment. Increased volatility tends to send investment community heads spinning as the Street tends to over-extrapolate everything. So we have a double whammy on stock prices; volatile earnings stream and more changeable expectations leading to bouncier PEs.
This and not scatter plots, is how you need to think about volatility; whichever kind you use (but if you use Beta, be careful not to underestimate the impact of the “relative to” qualifier.
As to the historical performance of low beta stocks, its just that, a report card that happened over specific time periods in the past. But unless you understand WHY it happened, you’re exposing your jaw (and bank accounts) to Mr. Market’s fists, and BTW, in case you haven’t noticed, Mr. Market, is s sh**load smarter — and tougher — than wannabe statisticians. Yeesh! After what we’ve been through in the last mont, I’d hope nobody around would want to debate that proposition.
Extremely wise comment, Marc. I think you and Hans Koolschijn are absolutely right and I really should have been looking at volatility from this angle all along. It’s very much like what you and I think about momentum. Stock prices reflect fundamentals and are secondary to them; judging stocks on their previous prices is never as good as judging them on their fundamentals (and sentiment signals), and looking at what prices tell us about fundamentals is more valuable than looking only at prices. It’s interesting that in all the academic literature I’ve read about the reasons for the “low-volatility anomaly” nobody has come up with your and Hans’s reasoning. That’s no excuse for me not thinking about it, though–call it a blind spot. Anyway, thanks for the correction. It’s never too late to learn from an old hand.
This is Marc Gerstein’s reply:
“It’s interesting that in all the academic literature I’ve read about the reasons for the “low-volatility anomaly” nobody has come up with your and Hans’s reasoning.”
Hans and I addressed the root causes of volatility. The anomaly is a different topic. This involves, why, in a particular period of observed time, lowval outperformed, contrary to what the theoretical principles might suggest. As best as I recall, it involved performance chasing that pushed too many managers to chase highvol, causing those stocks to become too richly valued to keep going. But the very recent value inversion might have reversed than the lowvol literature I’v seen predates the recent inversion.
Ultimately, one can drive one’s self crazy with too much factor performance study. At some point, you just have to say, based on financial theory, that this is supposed to happen, data (“evidence”) be damned. If reality turns out differently, the task becomes to explain why things turned out as they did and if it didn’t play out on script, that’s a cue to search for reasons so one can figure out what to do next; simply announcing the existence of an anomaly is a great way for a professor to publish something and avoid perishing, but for investors, it’s useless (best case) or dangerous (worst case) because it misleads people. into believing the observed state of affairs is more enduring than it really is.
The term evidence-based investing is very badly misused, In law, there are many instances in which evidence is inadmissible (even if accurate). The first requirement for admissibility is relevance. But even if relevant, evidence may still be excluded if the potential inflammatory impact exceeds its probative value. Much of the quant literature I’ve seen fails the second test, and a surprising amount even botches test 1. (In this context, inflammatory should be edited to read danger of lulling readers into believing a phenomenon is more real than it really is. (The small cap effect is a huge example of literature that should never have been published based on this principle.)
I think it’s probable that the reason that low vol has outperformed is precisely because what you and Hans identified as the root causes of low vol are things that would naturally cause a company to outperform expectations. I intend to go into this more thoroughly in a future article.