
How to Be a Great Investor, Part Two: Understand Value
This article is the second in a ten-part series loosely based on Michael J. Mauboussin’s white paper “Thirty Years: Reflections on the Ten Attributes of Great Investors.” For the first part, see “How To Be A Great Investor, Part One: Be Numerate.” Please note: in this article, I’m departing from Mauboussin’s ideas at a number of junctures.
The Intrinsic Value of an Object
Obviously, an orange has some intrinsic value. It is nutritious and tasty and can be used in a variety of ways. It has value on its own and has value as an ingredient. But what is that value? Fifty cents? Three dollars?
When we go to a grocery store and buy oranges, we can imagine saying to ourselves, wow, oranges are cheap today, or oranges are expensive here! We have some notion of how much an orange should cost. How do we get that notion? From experience and from comparison. We’ve bought oranges before; or, if we haven’t, we’ve bought apples and plums and lemons and bananas.
What I’m getting at is this: intrinsic value can only very rarely be stated in terms of dollars and cents. It’s instead a range, and it’s arrived at through comparison and experience.
The Intrinsic Value of an Investment
When we determine a fair price to pay for a bond, we consider the following variables: the coupon payments, the market rate, the number of periods per year, the number of years to maturity, and the face value of the bond.
Generally speaking, these same factors—income, payment schedule, market rate, duration, and value upon maturity or sale—are the factors in play for every investible asset, from real estate to collectibles to stocks (although for many investments, such as collectibles, there may be no income or payment schedule, and for others, such as life annuities, there’s no value upon maturity). To understand value, the questions are simple (I’m quoting Mauboussin here):
- What will the cash flows be?
- When will I receive them?
- How risky are they?
But with stocks, we have no idea what the coupon payments, the market rate, the face value, or the number of years to maturity are. It’s much harder to determine a stock’s fair value than it is to determine a bond’s.
Applying this model to stocks is the basis for the dividend discount model. The fair value of a stock is the sum of its dividends over the length of holding it and its final value, discounted by a certain rate. The problem with this idea is that a lot of stocks that are worth investing in do not pay dividends, so this covers only a fraction of possible stocks to buy; in addition, this model favors stocks with unsustainably high dividend yields.
Many investors therefore treat stocks as if they are collectibles. They’ll think, for example, that a certain company is probably going to grow to ten times its present worth due to some quirky trait or an expectation of consumer demand. Others think of stock investments as safe places to park their money for the long run, disregarding value and simply buying stocks in the largest companies, trusting that because they’ve been so successful in the past, they’ll continue to be successful in the future. Yet others believe in the efficient market hypothesis (in which intrinsic and market value are equal) and/or the capital asset pricing model and/or the Fama-French five-factor model and/or some other version of econometrics.
These may be fine ideas and strategies, but they’re really not about value.
The Intrinsic Value of a Company
If you’re acquiring an entire company, there are basically eight different ways to determine the price you’re willing to pay. In alphabetical order:
- You could do a comparison analysis (or precedent transaction analysis) by looking at recent acquisitions of similar companies and comparing those to this one.
- You could use the discounted cash flow method, which is derived from investment valuation as outlined above, and about which I’ll write more below.
- If it’s a public company, you could simply value it at its current enterprise value (though you’d want to adjust that upwards a little, considering the effect of a takeover offer on the stock’s price). This is basically the sum of the market value of the company and its debt, minus any cash it has on hand. In this case, the current price of the stock is an important factor in determining a value for the company.
- You could do a leveraged buyout (LBO) analysis. The factors here are the required return for the financial sponsor and the appropriate debt-to-equity ratio.
- You could ascertain its liquidation value. (This is not the same as the company’s book value, as it is the sum of the market value of its assets.)
- You could do multiples analysis, in which you look at the P/E, P/S, and so on of comparable companies to determine a reasonable valuation.
- You could try to calculate its replication value by estimating the amount of cash you’d need to build the company from the ground up.
- And then there’s the strategy-based valuation: what difference will acquiring this company make to your business strategy? How much do you want to pay for it in order to transform your business? If it’s a competitor, you might be willing to pay a lot for it in order to decrease competition.
Ideally, most acquirers will combine more than one of these methods. But all acquirers of public companies are also going to take into consideration the market value of the company’s equity, or else they’ll never get the deal approved by the shareholders.
Can a Company’s Intrinsic Value Be Negative?
Let’s say you’re shopping for a used car. You find one that you fall in love with and buy it. But it needs work. Over the next two months, you spend $4,000 fixing it up. But then, over the following two months, the carburetor, the engine, and the clutch all suffer fatal failures. You decide to sell the car, but the best price you can get for it is $1,000. How much was the car worth originally? Considering you lost $3,000 on top of the purchase price, you shouldn’t have bought the car at all and, in fact, you should have been paid $3,000 for owning it.
The same is true for a business. Many businesses cannot run only on internally generated capital. They require investment. Whenever a new owner buys an existing business, there’s a chance she will lose more than she paid for it if the business fails. The net present value of the business, in that case, was a negative one at the time of purchase.
The Intrinsic Value of a Stock
Once you have figured out the intrinsic value of a company, you subtract its debt, preferred stock, and non-controlling interest, add its cash, and then divide that by the number of fully diluted shares. It’s really that simple. But figuring out the intrinsic value of the company isn’t.
Discounted Cash Flow Analysis
(The next two sections are quite technical. If you have no interest in DCF analysis, please feel free to skip them. There’s more to read later.)
Let’s look closely at discounted cash flow analysis for a moment, because Mauboussin has written a great deal about it. If the intrinsic value of a company is determined by the sum of its free cash flows and its final value, all discounted by the market rate, then one should be able to find companies whose intrinsic value differs substantially from their market value and, by investing in those that are comparatively cheap, make money.
The basic idea behind DCF analysis is as follows. We start with a basic equation called Gordon’s Growth Model, P = D / (r – g), where P is price, D is dividend, r is the required rate of return, and g is the growth of dividends over time. There’s a very elegant proof of this equation, which you can read about here.
Because most stocks don’t pay dividends, however, investors have substituted free cash flow for D, and because cash flow and growth rates change over time, and because the “required rate of return” is so amorphous, they’ve expanded the model into a multi-year, hugely complicated mess. (But nobody ever said valuation should be easy.)
There are a number of major problems with DCF analysis.
- Determining cash flows. There is no clear method for determining future cash flows. I must have come across at least a dozen of them. (Mauboussin’s is explained in a book he co-wrote with Alfred Rappaport called Expectations Investing.) Most of them involve inputting a lot of guesses. There isn’t even a standard way to measure present free cash flows. Many analysts use different formulae from those provided by the CFA Institute. A big question is how to calculate maintenance capital expenditures (as distinguished from those that contribute to growth); if one deducts all capital expenditures from operating cash flow, then certain industries, such as utilities, have overall negative cash flows. And then there’s the problem exemplified by Hertz (HTZ), in which a company with a market cap of $1.25 billion has maintenance capital expenditures of $10 to $12 billion a year (the amount it spends on new cars), resulting in massively negative free cash flows.
- Variability of free cash flow. Free cash flow is probably the most variable of all value measures. I measured this on Portfolio123 using a pretty wide universe of over 4,000 stocks: the median absolute percentage deviation of EPS over the last five years is 58%, while the same of free cash flow is 73%.
- Applying growth rates to negative numbers. If one takes a negative number and multiplies it by one plus a growth rate, one comes up with an even more negative number. And a large number of companies have negative free cash flows.
- Determining the cost of capital. There’s no standard way to calculate the cost of capital, which determines the discount rate (the required rate of return), a huge factor in DCF analysis.
- Determining the terminal value. There seems to be no agreement on which of two very different methods an investor should use: the perpetuity growth model or the EV/EBIDTA multiple model. Most academics insist on the former; most investors use the latter. There are problems with both. The perpetuity growth model is based on the sixth or eleventh year’s free cash flow, which is a wild guess to begin with, and is then divided by the difference between the cost of capital and the terminal growth rate, both of which are more wild guesses. The multiples model has all the problems of conventional valuations like P/E and P/S, and the way it’s often applied means that the terminal value ends up making up about 80% or 90% of the eventual valuation, which negates the whole idea behind DCF analysis.
- Discrepancies in cost of capital. Most people assign different costs of capital to companies in different industries. So let’s take two companies with exactly the same free cash flow, growth rates, and debt to equity ratios. If the first company is a utility and the second is a technology firm, the first’s cost of capital is about 4.5% and the second’s is about 10%. Let’s assume that the initial growth rate for both companies is 10% and it decreases every year until in year 6 it’s 3%, and that after the tenth year we calculate the final value of the firm based on that final growth rate of 3% and a discount rate equal to the cost of capital. The intrinsic value of the utility will be 4.5 times the intrinsic value of the technology firm. (The discrepancy will be even higher if you stop after five years or if your growth rate for the first five years remains constant.) Does that really make sense? It does if you’re taking into account the risk of investing in each company—clearly the utility is far less risky. But it makes no sense if you’re trying to find bargains. In the latter case, you want to invest in the cheapest companies, and the two companies should have the same intrinsic value. Or does the technology company really need to produce four times the amount of cash flow than the utility to make up for its greater cost of capital?
- Close-to-zero denominators. In the perpetual growth method of calculating the “terminal value” of the firm, one divides the final projected free cash flow by the difference between the weighted average cost of capital (WACC) and the terminal growth rate of the firm. The terminal growth rate is usually pegged to inflation and GDP growth, while the cost of debt is usually pegged to the interest rate on BBB-rated bonds. Currently, the interest rate on these bonds, after deducting for taxes, is lower than the twenty-year average of GDP growth. Thus the final projected free cash flow of a very heavily indebted company is going to be divided by a fraction of 1%, or multiplied by more than a hundred. This problem extends to other companies with low costs of capital; often the difference is between one and three percent, thus providing a multiplier between thirty-three and a hundred. Just a fraction of a percentage change in the terminal growth rate or the WACC will result in a huge change in terminal value.
- Market neutrality is unrealistic. Discounted free cash flow analysis usually pretends to be market neutral. In many methods, there’s not a single factor in the process that reflects the value that the market has currently assigned to the company. Mauboussin defends this stance ardently. But if you look at the price that acquirers actually pay for public companies, there’s a very strong correlation with market price. (I must issue a warning here. There are some major financial firms out there who only pretend to assign a “fair price” to securities based on discounted cash flow analysis. Anytime you see a fair price analysis that, over time, hews very closely to the market price, you can be sure it’s not strictly based on DCF analysis, which will usually give you results that veer very far from the market price.)
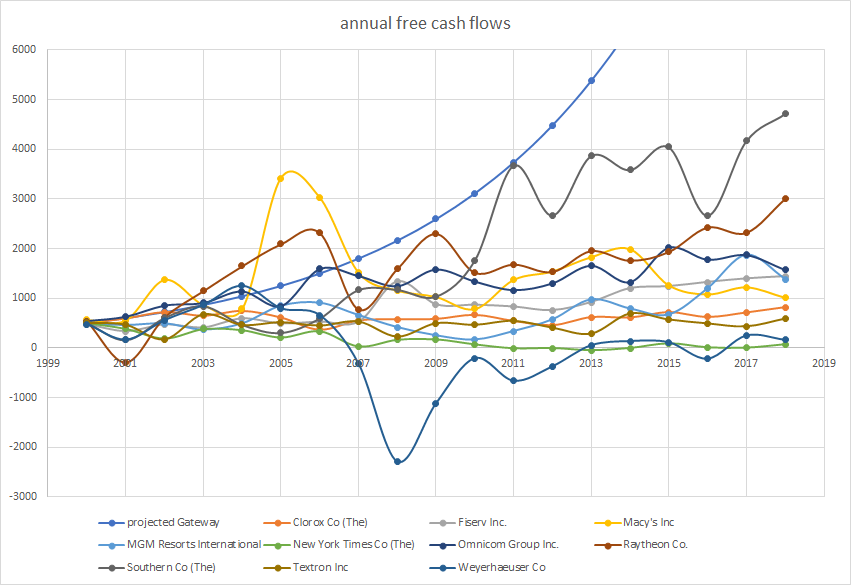
- Unrealistic future projections. DCF analysis relies too much on the future and not enough on the past and present. Take, for example, the company that Mauboussin and Rappaport used as their prime example when they wrote their book: Gateway, Inc. After analyzing this company in great detail and projecting future free cash flows, their spreadsheet, dated April 2000, predicted that over the next seven years the company’s cash flow would continue to increase. But Gateway’s cash flow plunged into negative numbers in 2001 and never recovered, and the stock’s price plunged from $52 to $2.20 over those years. In most examples of discounted cash flow analysis, free cash flow follows a smooth curve, based on sales growth expectations that are unsustainable. In real life, that rarely happens. Below is a chart of ten companies whose free cash flow in 2000 was about the same as Gateway’s. I’ve contrasted Gateway’s projected free cash flow, according to Mauboussin and Rappaport’s analysis, with the actual free cash flow (in millions) of these other ten companies. The difference is clear. Free cash flow varies hugely from year to year, and never conforms to a simple exponential curve.
Solutions to DCF problems
For my own DCF analysis, I’ve tried to come up with solutions to each of these problems. How well I’ve succeeded will be up to you to judge.
- Determining future free cash flows. I start with the following formula. Unlevered free cash flow (or free cash flow to the firm) is operating cash flow minus capital expenditures plus after-tax interest expense. But because one should only subtract maintenance capex, I add back a very rough estimate of growth capex, using Bruce Greenwald’s suggestion, which is the average ratio of gross plant to sales times the annual increase in sales. In many cases (Hertz being a good example), capital expenditures need to be offset by other cash flows from investing activities—Hertz’s capital expenditures consist of vehicle purchases, and its other cash flows partially offset that with vehicle sales. As for future free cash flows, there’s a weak but real correlation between future free cash flow growth and historical asset turnover, so I use a complicated formula based on the latter measure to estimate an initial growth rate.
- Variability of free cash flow. I use a weighted average of unlevered free cash flow, giving more weight to recent figures than those from the distant past. Using only trailing twelve-month numbers won’t get you much consistency, and using five-year averages ignores recent changes in cash flow generation.
- Applying growth rates to negative numbers. I add to the previous period’s free cash flow the greater of two numbers: the growth rate times the previous period’s free cash flow, and the growth rate times a small percentage of the company’s sales. This way a company with negative free cash flow but a positive growth rate will have a higher free cash flow number each year.
- Determining the cost of capital. The cost of capital (or WACC) is the weighted average of the cost of debt and the cost of equity, weighted according to the market value of the company’s debt and equity. I have estimated the cost of debt by looking at bond ratings for the industry group to which the company belongs, which are often significantly worse than BBB. The cost of equity is notoriously difficult to estimate. The basic formula is to take a risk-free rate based on the payment of ten-year treasury bonds, add an equity risk premium, and multiply the premium by the stock’s beta. Determining the equity risk premium is a wild guessing game, and stocks have crazily variable betas if measured by conventional means. I determine the equity risk premium by using the following formula: ERP = D*(1 + G) / P + G – Rf, where D is levered free cash flow (unlevered free cash flow minus interest expense plus debt increase), G is the terminal growth rate (the average of the projected inflation rate and long-term GDP growth), P is the market value of equity, and Rf is the risk-free rate (ten-year treasury bonds). So by looking at the sum of all companies’ levered free cash flow and the total value of the market, one can arrive at a reasonable premium (by my calculation, it’s 7.22%). I then multiply that by the twenty-year beta of the industry group the stock is in, measured according to weekly returns, which is a far more stable and reasonable number than the monthly beta of an individual stock over the last five years.
- Determining the terminal value. I have chosen to use the EV/EBITDA multiples method. It has some problems, but I’ve taken measures to reduce those by making extensive modifications to the method. Considering that the discount rates I use average around eight or nine percent and the terminal value is not applied until the eleventh year, the balance between the contributions of free cash flow and EBITDA to the intrinsic value is about even.
- Discrepancies in cost of capital. The average cost of capital of a utility company is 4.75% and the average cost of capital of a semiconductor manufacturer is 12%, which remains a very large discrepancy. But my emphasis on EV/EBITDA multiples in my method reduces this discrepancy to a large degree, especially since the multiple for utilities averages about 10 and the multiple for semiconductors averages about 13.
- Close-to-zero denominators. Since I don’t use the perpetual growth terminal value, which is where this problem really asserts itself, this isn’t a problem for me. But if you do use that, I recommend using the WACC for the entire industry group rather than for the particular stock. In addition, for the cost of debt I typically use the B bond rate rather than the BBB rate (except for certain very safe industries), so this would really only be a problem for utilities, as they have by far the lowest cost of capital.
- Market neutrality is unrealistic. I use an EV/EBITDA multiple in my terminal value estimate. This multiple I base on the current multiple of all stocks, the current multiple of the stocks in the particular industry group (but only those that are over ten years old), and the historical multiple of the particular stock. Thus my intrinsic value estimate is not market neutral.
- Unrealistic future projections. The key to solving this problem is to apply strict maximums and minimums to one’s initial growth projection and then to weight the average of that projection after the first year with the terminal growth number (3%) until, after five years or so, you’re simply using the latter.
Ben Graham on Intrinsic Value
Benjamin Graham and David L. Dodd dealt with many of the problems of value analysis forthrightly in their masterpiece, Security Analysis, a book which should be in every great investor’s library. It’s worth quoting them at length:
We must recognize . . . that intrinsic value is an elusive concept. In general terms it is understood to be that value which is justified by the facts, e.g., the assets, earnings, dividends, definite prospects, as distinct, let us say, from market quotations established by artificial manipulation or distorted by psychological excesses. But it is a great mistake to imagine that intrinsic value is as definite and as determinable as is the market price. . . .
[The] concept of intrinsic value, as . . . definite and ascertainable, cannot be safely accepted as a general premise of security analysis. . . .
The essential point is that security analysis does not seek to determine exactly what is the intrinsic value of a given security. It needs only to establish either that the value is adequate—e.g., to protect a bond or to justify a stock purchase—or else that the value is considerably higher or considerably lower than the market price. . . .
To express the uncertainty of the picture, we might say that it was difficult to determine in 1933 whether the intrinsic value of Case common was nearer $30 or $130. Yet if the stock had been selling at as low as $10, the analyst would undoubtedly have been justified in declaring that it was worth more than the market price. . . .
It would follow that even a very indefinite idea of the intrinsic value may still justify a conclusion if the current price falls far outside either the maximum or minimum appraisal.
Benjamin Graham and David L. Dodd
Expected Net Present Value
Net present value is the present value of future cash flows and is at the heart of discounted cash flow analysis. It is widely used throughout the financial industry, by appraisers, accountants, bankers, analysts, and many others. But a variation of it is widely used as well, and it is variously labeled “expected net present value” and “risk-adjusted net present value.” Basically, this method takes the best- and worst-case scenarios and provides a range of net present values. One can weight these probabilistically to come up with one net present value, or one can accept the entire range as possibilities. The latter is the approach Graham and Dodd were clearly in favor of. As long as a security is within that range, it can be said to be fairly priced.
Fairly Priced, Overvalued, and Undervalued Stocks
As noted, I’ve developed complicated formulae for calculating the intrinsic value of stocks. I think, though I’m not entirely sure, that the formulae perform better, on the whole, than using comparative measures like price-to-sales or price-to-forward-earnings. At any rate, it’s gratifying to see what numbers they spit out.
If you use those formulae to get the intrinsic value of S&P 500 stocks and set outer bounds at 50% and 200% of that value, close to 400 of those 500 stocks can be classified as “fairly priced.” I won’t claim, however, that the undervalued stocks are especially likely to increase in price or that the overvalued stocks are especially likely to decrease. A lot of other factors go into that.
Expectations and Value
While understanding value may be essential for great investors of Mauboussin’s stripe, there have been other great investors—including T. Rowe Price and Ed Thorp—who paid very little attention to (intrinsic) value. One can actually invest quite profitably without even looking at a company’s price at all.
In an article called “A Universal Theory of Stock Market Investing,” I wrote that a stock has no intrinsic value; its value is simply what the market says it is at any moment, and one can use various measures to predict which stocks will increase and which will decrease in value. I was wrong. The problem with this view is that it utterly fails to explain why when we buy an orange, we’re not going to pay $20 for it. Nothing is without intrinsic value, and that value can’t be entirely unmoored from market value.
But its intrinsic value should never be the only reason to buy or sell a stock. It’s better to focus on the probability that a stock will rise in price due to changes in investor expectations. And Mauboussin insists that this is the real key to valuation: “At the end of the day, we can prove very little about valuation. The reason is simple: stock prices (and the inputs that derive them) reflect investor expectations. Changes in investor expectations, in turn, largely dictate total shareholder returns.”
Value Drivers
Many dozens of factors drive changes in investor expectations. These are often called value drivers.
If you look at what could change a company’s intrinsic value, the most obvious thing is free cash flow. Anything conducive to increasing operating cash flow or reducing maintenance capital expenditures over the very long haul is therefore a value driver.
Reducing a company’s cost of capital will also drive value, and the easiest way for a company to do this is through share buybacks. (Increasing debt will also drive value if you look purely at intrinsic value, since it also decreases the cost of capital. But at the same time it significantly increases the company’s current enterprise value, thereby reducing its discount to intrinsic value.)
Obviously, increasing revenue will drive value, and most companies are focused on that as their primary goal. But revenue allocation involves a host of strategic decisions, many of which will end up destroying rather than driving value.
And that will be the subject of my next article in this series.

4 Replies to “How to Be a Great Investor, Part Two: Understand Value”